Peerannot: classification for crowdsourced image datasets with Python

1 Introduction: crowdsourcing in image classification

Image datasets widely use crowdsourcing to collect labels, involving many workers who can annotate images for a small cost (or even free for instance in citizen science) and faster than using expert labeling. Many classical datasets considered in machine learning have been created with human intervention to create labels, such as CIFAR-10, (Krizhevsky and Hinton 2009), ImageNet (Deng et al. 2009) or Pl@ntnet (Garcin et al. 2021) in image classification, but also COCO (Lin et al. 2014), solar photovoltaic arrays (Kasmi et al. 2023) or even macro litter (Chagneux et al. 2023) in image segmentation and object counting.

Crowdsourced datasets induce at least three major challenges to which we contribute with peerannot:

1. How to aggregate multiple labels into a single label from crowdsourced tasks? This occurs for example when dealing with a single dataset that has been labeled by multiple workers with disagreements. This is also encountered with other scoring issues such as polls, reviews, peer-grading, etc. In our framework this is treated with the aggregate command, which given multiple labels, infers a label. From aggregated labels, a classifier can then be trained using the train command.
2. How to learn a classifier from crowdsourced datasets? Where the first question is bound by aggregating multiple labels into a single one, this considers the case where we do not need a single label to train on, but instead train a classifier on the crowdsourced data, with the motivation to perform well on a testing set. This end-to-end vision is common in machine learning, however, it requires the actual tasks (the images, texts, videos, etc.) to train on – and in crowdsourced datasets publicly available, they are not always available. This is treated with the aggregate-deep command that runs strategies where the aggregation has been transformed into a deep learning optimization problem.
3. How to identify good workers in the crowd and difficult tasks? When multiple answers are given to a single task, looking for who to trust for which type of task becomes necessary to estimate the labels or later train a model with as few noise sources as possible. The module identify uses different scoring metrics to create a worker and/or task evaluation. This is particularly relevant considering the gamification of crowdsourcing experiments (Servajean et al. 2016)

The library peerannot addresses these practical questions within a reproducible setting. Indeed, the complexity of experiments often leads to a lack of transparency and reproducible results for simulations and real datasets. We propose standard simulation settings with explicit implementation parameters that can be shared. For real datasets, peerannot is compatible with standard neural network architectures from the Torchvision (Marcel and Rodriguez 2010) library and Pytorch (Paszke et al. 2019), allowing a flexible framework with easy-to-share scripts to reproduce experiments.

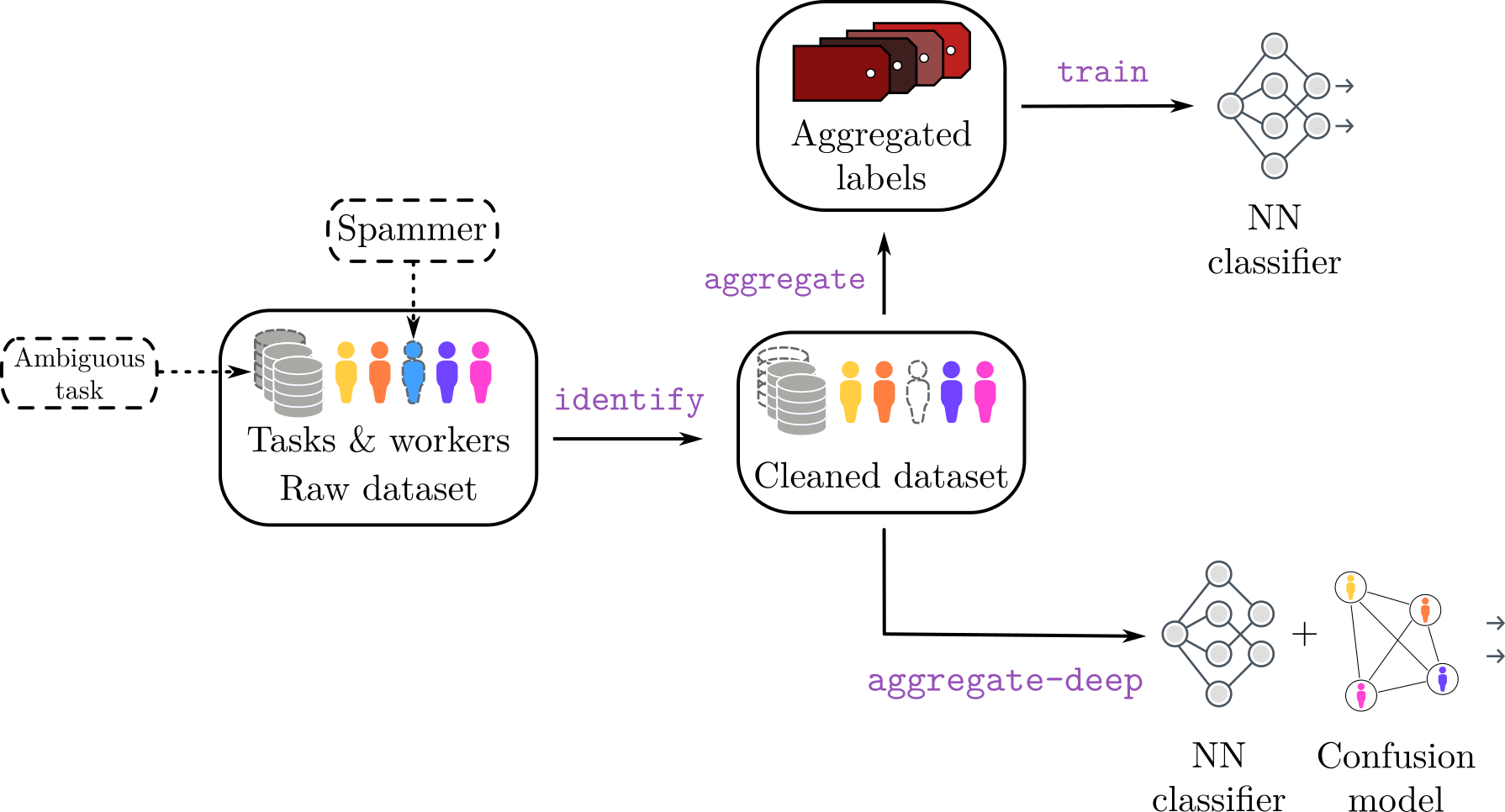
Figure 1: From crowdsourced labels to training a classifier neural network, the learning pipeline using the peerannot library. An optional preprocessing step using the identify command allows us to remove the worst-performing workers or images that can not be classified correctly (very bad quality for example). Then, from the cleaned dataset, the aggregate command may generate a single label per task from a prescribed strategy. From the aggregated labels we can train a neural network classifier with the train command. Otherwise, we can directly train a neural network classifier that takes into account the crowdsourcing setting in its architecture using aggregate-deep.

2 Notation and package structure

2.1 Crowdsourcing notation

Let us consider the classical supervised learning classification framework. A training set \mathcal{D}=\{(x_i, y_i^\star)\}_{i=1}^{n_{\text{task}}} is composed of n_{\text{task}} tasks x_i\in\mathcal{X} (the feature space) with (unknown) true label y_i^\star \in [K]=\{1,\dots,K\} one of the K possible classes. In the following, the tasks considered are generally RGB images. We use the notation \sigma(\cdot) for the softmax function. In particular, given a classifier \mathcal{C} with logits outputs, \sigma(\mathcal{C}(x_i))_{[1]} represents the largest probability and we can sort the probabilities as \sigma(\mathcal{C}(x_i))_{[1]}\geq \sigma(\mathcal{C}(x_i))_{[2]}\geq \dots\geq \sigma(\mathcal{C}(x_i))_{[K]}. The indicator function is denoted \mathbf{1}(\cdot). We use the i index notation to range over the different tasks and the j index notation for the workers in the crowdsourcing experiment. Note that indices start at position 1 in the equation to follow mathematical standard notation but it should be noted that, as this is a Python library, in the code indices start at the 0 position.

With crowdsourced data the true label of a task x_i, denoted y_i^\star is unknown, and there is no single label that can be trusted as in standard supervised learning (even on the train set!). Instead, there is a crowd of n_{\text{worker}} workers from which multiple workers (w_j)_j propose a label (y_i^{(j)})_j. These proposed labels are used to estimate the true label. The set of workers answering the task x_i is denoted by \mathcal{A}(x_i)=\left\{j\in[n_\text{worker}]: w_j \text{ answered }x_i\right\}. \tag{1}

The cardinal \vert \mathcal{A}(x_i)\vert is called the feedback effort on the task x_i. Note that the feedback effort can not exceed the total number of workers n_{\text{worker}}. Similarly, one can adopt a worker point of view: the set of tasks answered by a worker w_j is denoted \mathcal{T}(w_j)=\left\{i\in[n_\text{task}]: w_j \text{ answered } x_i\right\}. \tag{2}

The cardinal \vert \mathcal{T}(w_j)\vert is called the workload of w_j. The final dataset can then be decomposed as: \mathcal{D}_{\text{train}} := \bigcup_{i\in[n_\text{task}]} \left\{(x_i, (y_i^{(j)})) \text{ for }j\in\mathcal{A}(x_i)\right\} = \bigcup_{j\in[n_\text{worker}]} \left\{(x_i, (y_i^{(j)})) \text{ for }i \in\mathcal{T}(w_j)\right\} \enspace.

In this article, we do not address the setting where workers report their self-confidence (Yasmin et al. 2022), nor settings where workers are presented a trapping set – i.e., a subset of tasks where the true label is known to evaluate them with known labels (Khattak 2017).

2.2 Storing crowdsourced datasets in peerannot

Crowdsourced datasets come in various forms. To store crowdsourcing datasets efficiently and in a standardized way, peerannot proposes the following structure, where each dataset corresponds to a folder. Let us set up a toy dataset example to understand the data structure and how to store it.

Listing 1: Dataset storage tree structure.

datasetname
      ├── train
      │     ├── ...
      │     ├── images
      │     └── ...
      ├── val
      ├── test
      ├── metadata.json
      └── answers.json

The answers.json file stores the different votes for each task as described in Figure 2. This .json is the rosetta stone between the task ids and the images. It contains the tasks’ id, the workers’s id and the proposed label for each given vote. Furthermore, storing labels in a dictionary is more memory-friendly than having an array of size (n_task,n_worker) and writing y_i^{(j)}=-1 when the worker w_j did not see the task x_i and y_i^{(j)}\in[K] otherwise.

Figure 2: Data storage for the toy-data crowdsourced dataset, a binary classification problem (K=2, smiling/not smiling) on recognizing smiling faces. (left: how data is stored in peerannot in a file answers.json, right: data collected)

In Figure 2, there are three tasks, n_{\text{worker}}=4 workers and K=2 classes. Any available task should be stored in a single file whose name follows the convention described in Listing 1. These files are spread into a train, val and test subdirectories as in ImageFolder datasets from torchvision

Finally, a metadata.json file includes relevant information related to the crowdsourcing experiment such as the number of workers, the number of tasks, etc. For example, a minimal metadata.json file for the toy dataset presented in Figure 2 is:

{
    "name": "toy-data",
    "n_classes": 2,
    "n_workers": 4,
    "n_tasks": 3
}

The toy-data example dataset is available as an example in the peerannot repository. Classical datasets in crowdsourcing such as \texttt{CIFAR-10H} (Peterson et al. 2019) and \texttt{LabelMe} (Rodrigues, Pereira, and Ribeiro 2014) can be installed directly using peerannot. To install them, run the install command from peerannot:

! peerannot install ./datasets/labelme/labelme.py
! peerannot install ./datasets/cifar10H/cifar10h.py

For both \texttt{CIFAR-10H} and \texttt{LabelMe}, the dataset was was originally released for standard supervised learning (classification). Both datasets has been reannotated by a crowd or workers. These labels are used as true labels in evaluations and visualizations. Examples of \texttt{CIFAR-10H} images are available in Figure 14, and \texttt{LabelMe} examples in Figure 15 in Appendix. Crowdsourcing votes, however, bring information about possible confusions (see Figure 3 for an example with \texttt{CIFAR-10H} and Figure 4 with \texttt{LabelMe}).

import torch
import seaborn as sns
import matplotlib.pyplot as plt
from PIL import Image
import numpy as np
from pathlib import Path
import json
import matplotlib.ticker as mtick
import pandas as pd
sns.set_style("whitegrid")
import utils as utx
utx.figure_5()

Figure 3: Example of crowdsourced images from CIFAR-10H. Each task has been labeled by multiple workers. We display the associated voting distribution over the possible classes.

utx.figure_5_labelmeversion()

Figure 4: Example of crowdsourced images from LabelMe. Each task has been labeled by multiple workers. We display the associated voting distribution over the possible classes.

3 Aggregation strategies in crowdsourcing

The first question we address with peerannot is: How to aggregate multiple labels into a single label from crowdsourced tasks? The aggregation step can lead to two types of learnable labels \hat{y}_i\in\Delta_{K} (where \Delta_{K} is the simplex of dimension K-1: \Delta_{K}=\{p\in \mathbb{R}^K: \sum_{k=1}^K p_k = 1, p_k \geq 0 \} ) depending on the use case for each task x_i, i=1,\dots,n_{\text{task}}:

• a hard label: \hat{y}_i is a Dirac distribution, this can be encoded as a classical label in [K],
• a soft label: \hat{y}_i\in\Delta_{K} can represent any probability distribution on [K]. In that case, each coordinate of the K-dimensional vector \hat{y}_i represents the probability of belonging to the given class.

Learning from soft labels has been shown to improve learning performance and make the classifier learn the task ambiguity (Zhang et al. 2018; Peterson et al. 2019; Park and Caragea 2022). However, crowdsourcing is often used as a stepping stone to create a new dataset. We usually expect a classification dataset to associate a task x_i to a single label and not a full probability distribution. In this case, we recommend releasing the anonymous answered labels and the aggregation strategy used to reach a consensus on a single label. With peerannot, both soft and hard labels can be produced.

Note that when a strategy produces a soft label, a hard label can be easily induced by taking the mode, i.e., the class achieving the maximum probability.

3.1 Classical models

We list below the most classical aggregation strategies used in crowdsourcing.

3.1.1 Majority vote (MV)

The most intuitive way to create a label from multiple answers for any type of crowdsourced task is to take the majority vote (MV). Yet, this strategy has many shortcomings (James 1998) – there is no noise model, no worker reliability estimated, no task difficulty involved and especially no way to remove poorly performing workers. This standard choice can be expressed as:

\hat{y}_i^{\text{MV}} = \operatornamewithlimits{argmax}_{k\in[K]} \sum_{j\in\mathcal{A}(x_i)} \mathbf{1}_{\{y_i^{(j)}=k\}} \enspace.

3.1.2 Naive soft (NS)

One pitfall with MV is that the label produced is hard, hence the ambiguity is discarded by construction. A simple remedy consists in using the Naive Soft (NS) labeling, i.e., output the empirical distribution as the task label:

\hat{y}_i^{\text{NS}} = \bigg(\frac{1}{\vert\mathcal{A}(x_i)\vert}\sum_{j\in\mathcal{A}(x_i)} \mathbf{1}_{\{y_i^{(j)}=k\}} \bigg)_{j\in[K]} \enspace. With the NS label, we keep the ambiguity, but all workers and all tasks are put on the same level. In practice, it is known that each worker comes with their abilities, thus modeling this knowledge can produce better results.

3.1.3 Dawid and Skene (DS)

Refining the aggregation, researchers have proposed a noise model to take into account the workers’ abilities. The Dawid and Skene’s (DS) model (Dawid and Skene 1979) is one of the most studied (Gao and Zhou 2013) and applied (Servajean et al. 2017; Rodrigues and Pereira 2018). These types of models are most often optimized using EM-based procedures. Assuming the workers are answering tasks independently, this model boils down to model pairwise confusions between each possible class. Each worker w_j is assigned a confusion matrix \pi^{(j)}\in\mathbb{R}^{K\times K} as described in Section 3. The model assumes that for a task x_i, conditionally on the true label y_i^\star=k the label distribution of the worker’s answer follows a multinomial distribution with probabilities \pi^{(j)}_{k,\cdot} for each worker. Each class has a prevalence \rho_k=\mathbb{P}(y_i^\star=k) to appear in the dataset. Using the independence between workers, we obtain the following likelihood to maximize, with latent variables \rho, \pi=\{\pi^{(j)}\}_{j} and unobserved variables (y_i^{(j)})_{i,j}: \arg\max_{\rho,\pi}\displaystyle\prod_{i\in [n_{\texttt{task}}]}\prod_{k \in [K]}\bigg[\rho_k\prod_{j\in [n_{\texttt{worker}}]} \prod_{\ell\in [K]}\big(\pi^{(j)}_{k, \ell}\big)^{\mathbf{1}_{\{y_i^{(j)}=\ell\}}} \bigg].

When the true labels are not available, the data comes from a mixture of categorical distributions. To retrieve ground truth labels and be able to estimate these parameters, Dawid and Skene (1979) have proposed to consider the true labels as additional unknown parameters. In this case, denoting T_{i,k}=\mathbf{1}_{\{y_i^{\star}=k \}} the vectors of label class indicators for each task, the likelihood with known true labels is: \arg\max_{\rho,\pi,T}\displaystyle\prod_{i\in [n_{\texttt{task}}]}\prod_{k \in [K]}\bigg[\rho_k\prod_{j\in [n_{\texttt{worker}}]} \prod_{\ell\in [K]}\big(\pi^{(j)}_{k, \ell}\big)^{\mathbf{1}_{\{y_i^{(j)}=\ell\}}} \bigg]^{T_{i,k}}.

This framework allows to estimate \rho,\pi,T with an EM algorithm as follows:

• With the MV strategy, get an initial estimate of the true labels T.
• Estimate \rho and \pi knowing T using maximum likelihood estimators.
• Update T knowing \rho and \pi using Bayes formula.
• Repeat until convergence of the likelihood.

The final aggregated soft labels are \hat{y}_i^{\text{DS}} = T_{i,\cdot}. Note that DS also provides the estimated confusion matrices \hat{\pi}^{(j)} for each worker w_j.

Bayesian plate notation for the DS model

3.1.4 Variations around the DS model

Many variants of the DS model have been proposed in the literature, using Dirichlet priors on the confusion matrices (Passonneau and Carpenter 2014), using 1\leq L\leq n_{\text{worker}} clusters of workers (Imamura, Sato, and Sugiyama 2018) (DSWC) or even faster implementation that produces only hard labels (Sinha, Rao, and Balasubramanian 2018).

In particular, the DSWC strategy (Dawid and Skene with Worker Clustering) highly reduces the dimension of the parameters in the DS model. In the original model, there are K^2\times n_{\text{worker}} parameters to be estimated for the confusion matrices only. The DSWC model reduces them to K^2\times L + L parameters. Indeed, there are L confusion matrices \Lambda=\{\Lambda_1,\dots,\Lambda_L\} and the confusion matrix of a cluster is assumed drawn from a multinomial distribution with weights (\tau_1,\dots,\tau_L)\in \Delta_{L} over \Lambda, such that \mathbb{P}(\pi^{(j)}=\Lambda_\ell)=\tau_\ell.

3.1.5 Generative model of Labels, Abilities, and Difficulties (GLAD)

Finally, we present the GLAD model (Whitehill et al. 2009) that not only takes into account the worker’s ability, but also the task difficulty in the noise model. The likelihood is optimized using an EM algorithm to recover the soft label \hat{y}_i^{\text{GLAD}}.

Bayesian plate notation for the GLAD model

Denoting \alpha_j\in\mathbb{R} the worker ability (the higher the better) and \beta_i\in\mathbb{R}^+_\star the task’s difficulty (the higher the easier), the model noise is:

\mathbb{P}(y_i^{(j)}=y_i^\star\vert \alpha_j,\beta_i) = \frac{1}{1+\exp(-\alpha_j\beta_i)} \enspace. GLAD’s model also assumes that the errors are uniform across wrong labels, thus: \forall k \in [K],\ \mathbb{P}(y_i^{(j)}=k\vert y_i^\star\neq k,\alpha_j,\beta_i) = \frac{1}{K-1}\left(1-\frac{1}{1+\exp(-\alpha_j\beta_i)}\right)\enspace. This results in estimating n_{\text{worker}} + n_{\text{task}} parameters.

3.1.6 Aggregation strategies in peerannot

All of these aggregation strategies – and more – are available in the peerannot library from the peerannot.models module. Each model is a class object in its own Python file. It inherits from the CrowdModel template class and is defined with at least two methods:

• run: includes the optimization procedure to obtain needed weights (e.g., the EM algorithm for the DS model),
• get_probas: returns the soft labels output for each task.

3.2 Experiments and evaluation of label aggregation strategies

One way to evaluate the label aggregation strategies is to measure their accuracy. This means that the underlying ground truth must be known – at least for a representative subset. This is the case in simulation settings where the ground truth is available. As the set of n_{\text{task}} can be seen as a training set for a future classifier, we denote this metric \operatornamewithlimits{AccTrain} on a dataset \mathcal{D} for some given aggregated label (\hat{y}_i)_i as:

\operatornamewithlimits{AccTrain}(\mathcal{D}) = \frac{1}{\vert \mathcal{D}\vert}\sum_{i=1}^{\vert\mathcal{D}\vert} \mathbf{1}_{\{y_i^\star=\operatornamewithlimits{argmax}_{k\in[K]}(\hat{y}_i)_k\}} \enspace.

In the following, we write \operatornamewithlimits{AccTrain} for \operatornamewithlimits{AccTrain}(\mathcal{D}_{\text{train}}) as we only consider the full training set so there is no ambiguity. The \operatornamewithlimits{AccTrain} computes the number of correctly predicted labels by the aggregation strategy knowing a ground truth. While this metric is useful, in practice there are a few arguable issues:

• the \operatornamewithlimits{AccTrain} metric does not consider the ambiguity of the soft label, only the most probable class, whereas in some contexts ambiguity can be informative,
• in supervised learning one objective is to identify difficult or mislabeled tasks (Pleiss et al. 2020; Lefort et al. 2022), pruning those tasks can easily artificially improve the \operatornamewithlimits{AccTrain}, but there is no guarantee over the predictive performance of a model based on the newly pruned dataset,
• in practice, true labels are unknown, thus this metric would not be computable.

We first consider classical simulation settings in the literature that can easily be created and reproduced using peerannot. For each dataset, we present the distribution of the number of workers per task (|\mathcal{A}(x_i)|)_{i=1,\dots, n_{\text{task}}}~ Equation 1 on the right and the distribution of the number of tasks per worker (|\mathcal{T}(w_j)|)_{j=1,\dots,n_{\text{worker}}} Equation 2 on the left.

3.2.1 Simulated independent mistakes

The independent mistakes setting considers that each worker w_j answers follows a multinomial distribution with weights given at the row y_i^\star of their confusion matrix \pi^{(j)}\in\mathbb{R}^{K\times K}. Each confusion row in the confusion matrix is generated uniformly in the simplex. Then, we make the matrix diagonally dominant (to represent non-adversarial workers) by switching the diagonal term with the maximum value by row. Answers are independent of one another as each matrix is generated independently and each worker answers independently of other workers. In this setting, the DS model is expected to perform better with enough data as we are simulating data from its assumed noise model.

We simulate n_{\text{task}}=200 tasks and n_{\text{worker}}=30 workers with K=5 possible classes. Each task x_i receives \vert\mathcal{A}(x_i)\vert=10 labels. With 200 tasks and 30 workers, asking for 10 leads to around \frac{200\times 10}{30}\simeq 67 tasks per worker (with variations due to randomness in the affectations).

! peerannot simulate --n-worker=30 --n-task=200  --n-classes=5 \
                     --strategy independent-confusion \
                     --feedback=10 --seed 0 \
                     --folder ./simus/independent

from peerannot.helpers.helpers_visu import feedback_effort, working_load
import matplotlib.pyplot as plt
from matplotlib.ticker import MaxNLocator
from pathlib import Path

votes_path = Path.cwd() / "simus" / "independent" / "answers.json"
metadata_path = Path.cwd() / "simus" / "independent" / "metadata.json"
efforts = feedback_effort(votes_path)
workload = working_load(votes_path, metadata_path)
feedback = feedback_effort(votes_path)
utx.figure_simulations(workload, feedback)
plt.show()

Figure 5: Distribution of number of tasks given per worker (left) and number of labels per task (right) in the independent mistakes setting.

With the obtained answers, we can look at the aforementioned aggregation strategies performance. The peerannot aggregate command takes as input the path to the data folder and the aggregation --strategy/-s to perform. Other arguments are available and described in the --help description.

for strat in ["MV", "NaiveSoft", "DS", "GLAD", "DSWC[L=5]", "DSWC[L=10]"]:
  ! peerannot aggregate ./simus/independent/ -s {strat}

import pandas as pd
import numpy as np
from IPython.display import display
simu_indep = Path.cwd() / 'simus' / "independent"
results = {
  "mv": [], "naivesoft": [], "glad": [],
  "ds": [], "dswc[l=5]": [], "dswc[l=10]": []
  }
for strategy in results.keys():
  path_labels = simu_indep / "labels" / f"labels_independent-confusion_{strategy}.npy"
  ground_truth = np.load(simu_indep / "ground_truth.npy")
  labels = np.load(path_labels)
  acc = (
          np.mean(labels == ground_truth)
          if labels.ndim == 1
          else np.mean(
              np.argmax(labels, axis=1)
              == ground_truth
          )
        )
  results[strategy].append(acc)
results["NS"] = results["naivesoft"]
results.pop("naivesoft")
results = pd.DataFrame(results, index=['AccTrain'])
results.columns = map(str.upper, results.columns)
results = results.style.set_table_styles(
  [dict(selector='th', props=[('text-align', 'center')])]
  )
results.set_properties(**{'text-align': 'center'})
results = results.format(precision=3)
display(results)

Table 1: AccTrain metric on simulated independent mistakes considering classical feature-blind label aggregation strategies

	MV	GLAD	DS	DSWC[L=5]	DSWC[L=10]	NS
AccTrain	0.765	0.775	0.890	0.775	0.770	0.760

As expected by the simulation framework, Table 1 fits the DS model, thus leading to better accuracy in retrieving the simulated labels for the DS strategy. The MV and NS aggregations do not consider any worker-ability scoring or the task’s difficulty and perform the worst.

Remark: peerannot can also simulate datasets with an imbalanced number of votes chosen uniformly at random between 1 and the number of workers available. For example:

! peerannot simulate --n-worker=30 --n-task=200  --n-classes=5 \
                     --strategy independent-confusion \
                     --imbalance-votes \
                     --seed 0 \
                     --folder ./simus/independent-imbalanced/

sns.set_style("whitegrid")

votes_path = Path.cwd() / "simus" / "independent-imbalanced" / "answers.json"
metadata_path = Path.cwd() / "simus" / "independent-imbalanced" / "metadata.json"
efforts = feedback_effort(votes_path)
workload = working_load(votes_path, metadata_path)
feedback = feedback_effort(votes_path)
utx.figure_simulations(workload, feedback)
plt.show()

Figure 6: Distribution of the number of tasks given per worker (left) and of the number of labels per task (right) in the independent mistakes setting with voting imbalance enabled.

With the obtained answers, we can look at the aforementioned aggregation strategies performance:

for strat in ["MV", "NaiveSoft", "DS", "GLAD", "DSWC[L=5]", "DSWC[L=10]"]:
  ! peerannot aggregate ./simus/independent-imbalanced/ -s {strat}

import pandas as pd
import numpy as np
from IPython.display import display
simu_indep = Path.cwd() / 'simus' / "independent-imbalanced"
results = {
  "mv": [], "naivesoft": [], "glad": [],
  "ds": [], "dswc[l=5]": [], "dswc[l=10]": []
  }
for strategy in results.keys():
  path_labels = simu_indep / "labels" / f"labels_independent-confusion_{strategy}.npy"
  ground_truth = np.load(simu_indep / "ground_truth.npy")
  labels = np.load(path_labels)
  acc = (
          np.mean(labels == ground_truth)
          if labels.ndim == 1
          else np.mean(
              np.argmax(labels, axis=1)
              == ground_truth
          )
        )
  results[strategy].append(acc)
results["NS"] = results["naivesoft"]
results.pop("naivesoft")
results = pd.DataFrame(results, index=['AccTrain'])
results.columns = map(str.upper, results.columns)
results = results.style.set_table_styles([dict(selector='th', props=[('text-align', 'center')])])
results.set_properties(**{'text-align': 'center'})
results = results.format(precision=3)
display(results)

Table 2: AccTrain metric on simulated independent mistakes with an imbalanced number of votes per task considering classical feature-blind label aggregation strategies

	MV	GLAD	DS	DSWC[L=5]	DSWC[L=10]	NS
AccTrain	0.840	0.810	0.895	0.845	0.840	0.830

While more realistic, working with an imbalanced number of votes per task can lead to disrupting orders of performance for some strategies (here GLAD is outperformed by other strategies).

3.2.2 Simulated correlated mistakes

The correlated mistakes are also known as the student-teacher or junior-expert setting (Cao et al. (2019)). Consider that the crowd of workers is divided into two categories: teachers and students (with n_{\text{teacher}} + n_{\text{student}}=n_{\text{worker}}). Each student is randomly assigned to one teacher at the beginning of the experiment. We generate the (diagonally dominant as in Section 3.2.1) confusion matrices of each teacher and the students share the same confusion matrix as their associated teacher. Hence, clustering strategies are expected to perform best in this context. Then, they all answer independently, following a multinomial distribution with weights given at the row y_i^\star of their confusion matrix \pi^{(j)}\in\mathbb{R}^{K\times K}.

We simulate n_{\text{task}}=200 tasks and n_{\text{worker}}=30 with 80\% of students in the crowd. There are K=5 possible classes. Each task receives \vert\mathcal{A}(x_i)\vert=10 labels.

! peerannot simulate --n-worker=30 --n-task=200  --n-classes=5 \
                     --strategy student-teacher \
                     --ratio 0.8 \
                     --feedback=10 --seed 0 \
                     --folder ./simus/student_teacher

votes_path = Path.cwd() / "simus" / "student_teacher" / "answers.json"
metadata_path = Path.cwd() / "simus" / "student_teacher" / "metadata.json"
efforts = feedback_effort(votes_path)
workload = working_load(votes_path, metadata_path)
feedback = feedback_effort(votes_path)
utx.figure_simulations(workload, feedback)
plt.show()

Figure 7: Distribution of number of tasks given per worker (left) and number of labels per task (right) in the correlated mistakes setting.

With the obtained answers, we can look at the aforementioned aggregation strategies performance:

for strat in ["MV", "NaiveSoft", "DS", "GLAD", "DSWC[L=5]", "DSWC[L=6]", "DSWC[L=10]"]:
  ! peerannot aggregate ./simus/student_teacher/ -s {strat}

simu_corr = Path.cwd() / 'simus' / "student_teacher"
results = {"mv": [], "naivesoft": [], "glad": [], "ds": [], "dswc[l=5]": [],
           "dswc[l=6]": [], "dswc[l=10]": []}
for strategy in results.keys():
  path_labels = simu_corr / "labels" / f"labels_student-teacher_{strategy}.npy"
  ground_truth = np.load(simu_corr / "ground_truth.npy")
  labels = np.load(path_labels)
  acc = (
          np.mean(labels == ground_truth)
          if labels.ndim == 1
          else np.mean(
              np.argmax(labels, axis=1)
              == ground_truth
          )
        )
  results[strategy].append(acc)
results["NS"] = results["naivesoft"]
results.pop("naivesoft")
results = pd.DataFrame(results, index=['AccTrain'])
results.columns = map(str.upper, results.columns)
results = results.style.set_table_styles(
  [dict(selector='th', props=[('text-align', 'center')])])
results.set_properties(**{'text-align': 'center'})
results = results.format(precision=3)
display(results)

Table 3: AccTrain metric on simulated correlated mistakes considering classical feature-blind label aggregation strategies

	MV	GLAD	DS	DSWC[L=5]	DSWC[L=6]	DSWC[L=10]	NS
AccTrain	0.710	0.645	0.755	0.795	0.780	0.815	0.690

With Table 3, we see that with correlated data (24 students and 6 teachers), using 5 confusion matrices with DSWC[L=5] outperforms the vanilla DS strategy that does not consider the correlations. The best-performing method here estimates only 10 confusion matrices (instead of 30 for the vanilla DS model).

To summarize our simulations, we see that depending on workers answering strategies, different latent variable models perform best. However, these are unknown outside of a simulation framework, thus if we want to obtain labels from multiple responses, we need to investigate multiple models. This can be done easily with peerannot as we demonstrated using the aggregate module. However, one might not want to generate a label, simply learn a classifier to predict labels on unseen data. This leads us to another module part of peerannot.

3.3 More on confusion matrices in simulation settings

Moreover, the concept of confusion matrices has been commonly used to represent worker abilities. Let us remind that a confusion matrix \pi^{(j)}\in\mathbb{R}^{K\times K} of a worker w_j is defined such that \pi^{(j)}_{k,\ell} = \mathbb{P}(y_i^{(j)}=\ell\vert y_i^\star=k). These quantities need to be estimated since no true label is available in a crowd-sourced scenario. In practice, the confusion matrices of each worker is estimated via an aggregation strategy like Dawid and Skene’s (Dawid and Skene 1979) presented in Section 3.1.

!peerannot simulate --n-worker=10 --n-task=100 --n-classes=5 \
  --strategy hammer-spammer --feedback=5 --seed=0 \
  --folder ./simus/hammer_spammer
!peerannot simulate --n-worker=10 --n-task=100 --n-classes=5 \
  --strategy independent-confusion --feedback=5 --seed=0 \
  --folder ./simus/hammer_spammer/confusion

mats = np.load("./simus/hammer_spammer/matrices.npy")
mats_confu = np.load("./simus/hammer_spammer/confusion/matrices.npy")

utx.figure_6(mats, mats_confu)

Figure 8: Three types of profiles of worker confusion matrices simulated with peerannot. The spammer answers independently of the true label. Expert workers identify classes without mistakes. In practice common workers are good for some classes but might confuse two (or more) labels. All workers are simulated using the peerannot simulate command presented in Section 3.2.

In Figure 8, we illustrate multiple workers’ profile (as reflected by their confusion matrix) on a simulate scenario where the ground truth is available. For that we generate toy datasets with the simulate command from peerannot. In particular, we display a type of worker that can hurt data quality: the spammer. Raykar and Yu (2011) defined a spammer as a worker that answers independently of the true label:

\forall k\in[K],\ \mathbb{P}(y_i^{(j)}=k|y_i^\star) = \mathbb{P}(y_i^{(j)}=k)\enspace. \tag{3}

Each row of the confusion matrix represents the label’s probability distribution given a true label. Hence, the spammer has a confusion matrix with near-identical rows. Apart from the spammer, common mistakes often involve workers mixing up one or several classes. Expert workers have a confusion matrix close to the identity matrix.

4 Learning from crowdsourced tasks

Commonly, tasks are crowdsourced to create a large annotated training set as modern machine learning models require more and more data. The aggregation step then simply becomes the first step in the complete learning pipeline. However, instead of aggregating labels, modern neural networks are directly trained end-to-end from multiple noisy labels.

4.1 Popular models

In recent years, directly learning a classifier from noisy labels was introduced. Two of the most used models: CrowdLayer (Rodrigues and Pereira 2018) and CoNAL (Chu, Ma, and Wang 2021), are directly available in peerannot. These two learning strategies directly incorporate a DS-inspired noise model in the neural network’s architecture.

4.1.1 CrowdLayer

CrowdLayer trains a classifier with noisy labels as follows. Let the scores (logits) output by a given classifier neural network \mathcal{C} be z_i=\mathcal{C}(x_i). Then CrowdLayer adds as a last layer \pi\in\mathbb{R}^{n_{\text{worker}}\times K\times K}, the tensor of all \pi^{(j)}’s such that the crossentropy loss (\mathrm{CE}) is adapted to the crowdsourcing setting into \mathcal{L}_{CE}^{\text{CrowdLayer}} and computed as:

\mathcal{L}_{CE}^{\text{CrowdLayer}}(x_i) = \sum_{j\in\mathcal{A}(x_i)} \mathrm{CE}\left(\sigma\left(\pi^{(j)}\sigma\big(z_i\big)\right), y_i^{(j)}\right) \enspace,

where the crossentropy loss for two distribution u,v \in\Delta_{K} is defined as \mathrm{CE}(u, v) = \sum_{k\in[K]} v_k\log(u_k).

Where DS modeled workers as confusion matrices, CrowdLayer adds a layer of \pi^{(j)}s into the backbone architecture as a new tensor layer to transform the output probabilities. The backbone classifier predicts a distribution that is then corrupted through the added layer to learn the worker-specific confusion. The weights in the tensor layer of \pi^{(j)}s are learned during the optimization procedure.

4.1.2 CoNAL

For some datasets, it was noticed that global confusion occurs between the proposed classes. It is the case for example in the \texttt{LabelMe} dataset (Rodrigues et al. 2017) where classes overlap. In this case, Chu, Ma, and Wang (2021) proposed to extend the CrowdLayer model by adding global confusion matrix \pi^g\in\mathbb{R}^{K\times K} to the model on top of each worker’s confusion.

Given the output z_i=\mathcal{C}(x_i)\in\mathbb{R}^K of a given classifier and task, CoNAL interpolates between the prediction corrected by local confusions \pi^{(j)}z_i and the prediction corrected by a global confusion \pi^gz_i. The loss function is computed as follows: \begin{aligned} &\mathcal{L}_{CE}^{\text{CoNAL}}(x_i) = \sum_{j\in\mathcal{A}(x_i)} \mathrm{CE}(h_i^{(j)}, y_i^{(j)}) \enspace, \\ &\text{with } h_i^{(j)} = \sigma\left(\big(\omega_i^{(j)} \pi^g + (1-\omega_i^{(j)})\pi^{(j)}\big)z_i\right) \enspace. \end{aligned} \

The interpolation weight \omega_i^{(j)} is unobservable in practice. So, to compute h_i^{(j)}, the weight is obtained through an auxiliary network. This network takes as input the image and worker information and outputs a task-related vector v_i and a worker-related vector u_j of the same dimension. Finally, w_i^{(j)}=(1+\exp(- u_j^\top v_i))^{-1}.

Both CrowdLayer and CoNAL model worker confusions directly in the classifier’s weights to learn from the noisy collected labels and are available in peerannot as we will see in the following.

4.2 Prediction error when learning from crowdsourced tasks

The \mathrm{AccTrain} metric presented in Section 3.2 might no longer be of interest when training a classifier. Classical error measurements involve a test dataset to estimate the generalization error. To do so, we present hereafter two error metrics. Assuming we trained our classifier \mathcal{C} on a training set and that there is a test set available with known true labels:

• the test accuracy is computed as \frac{1}{n_{\text{test}}}\sum_{i=1}^{n_{\text{test}}}\mathbf{1}_{\{y_i^\star = \hat{y}_i\}}.
• the expected calibration error (Guo et al. 2017) over M equally spaced bins I_1,\dots,I_M partitionning the interval [0,1], is computed as: \mathrm{ECE} = \sum_{m=1}^M \frac{|B_m|}{n_{\text{task}}}|\mathrm{acc}(B_m) - \mathrm{conf}(B_m)|\enspace, with B_m=\{x_i| \mathcal{C}(x_i)_{[1]}\in I_m\} the tasks with predicted probability in the m-th bin, \mathrm{acc}(B_m) the accuracy of the network for the samples in B_m and \mathrm{conf}(B_m) the associated empirical confidence. More precisely: \mathrm{acc}(B_m) = \frac{1}{|B_m|}\sum_{i\in B_m} \mathbf{1}(\hat{y}_i=y_i^\star)\quad \text{and} \quad \mathrm{conf}(B_m) = \frac{1}{|B_m|}\sum_{i\in B_m} \sigma(\mathcal{C}(x_i))_{[1]}\enspace.

The accuracy represents how well the classifier generalizes, and the expected calibration error (ECE) quantifies the deviation between the accuracy and the confidence of the classifier. Modern neural networks are known to often be overconfident in their predictions (Guo et al. 2017). However, it has also been remarked that training on crowdsourced data, depending on the strategy, mitigates this confidence issue. That is why we propose to compare them both in our coming experiments. Note that the ECE error estimator is known to be biased (Gruber and Buettner 2022). Smaller training sets are known to have a higher ECE estimation error. And in the crowdsourcing setting, openly available datasets are often quite small.

4.3 Use case with peerannot on real datasets

Few real crowdsourcing experiments have been released publicly. Among the available ones, \texttt{CIFAR-10H} (Peterson et al. 2019) is one of the largest with 10 000 tasks labeled by workers (the testing set of CIFAR-10). The main limitation of \texttt{CIFAR-10H} is that there are few disagreements between workers and a simple majority voting already leads to a near-perfect \mathrm{AccTrain} error. Hence, comparing the impact of aggregation and end-to-end strategies might not be relevant (Peterson et al. 2019; Aitchison 2021), it is however a good benchmark for task difficulty identification and worker evaluation scoring. Each of these dataset contains a test set, with known ground truth. Thus, we can train a classifier from the crowdsourced data, and compare predictive performance on the test set.

The \texttt{LabelMe} dataset was extracted from crowdsourcing segmentation experiments and a subset of K=8 classes was released in Rodrigues et al. (2017).

Let us use peerannot to train a VGG-16 with two dense layers on the \texttt{LabelMe} dataset. Note that this modification was introduced to reach state-of-the-art performance in (Chu, Ma, and Wang 2021). Other models from the torchvision library can be used, such as Resnets, Alexnet etc. The aggregate-deep command takes as input the path to the data folder, --output-name/-o is the name for the output file, --n-classes/-K the number of classes, --strategy/-s the learning strategy to perform (e.g., CrowdLayer or CoNAL), the backbone classifier in --model and then optimization hyperparameters for pytorch described with more details using the peerannot aggregate-deep --help command.

for strat in ["MV", "NaiveSoft", "DS", "GLAD"]:
  ! peerannot aggregate ./labelme/ -s {strat}
  ! peerannot train ./labelme -o labelme_${strat} \
    -K 8 --labels=./labelme/labels/labels_labelme_${strat}.npy \
    --model modellabelme --n-epochs 500 -m 50 -m 150 -m 250 \
    --scheduler=multistep --lr=0.01 --num-workers=8 \
    --pretrained --data-augmentation --optimizer=adam \
    --batch-size=32 --img-size=224 --seed=1
for strat in ["CrowdLayer", "CoNAL[scale=0]", "CoNAL[scale=1e-4]"]:
  ! peerannot aggregate-deep ./labelme -o labelme_${strat} \
    --answers ./labelme/answers.json -s ${strat} --model modellabelme \
    --img-size=224 --pretrained --n-classes=8 --n-epochs=500 --lr=0.001 \
    -m 300 -m 400 --scheduler=multistep --batch-size=228 --optimizer=adam \
    --num-workers=8 --data-augmentation --seed=1


# command to save separately a specific part of CoNAL model (memory intensive otherwise)
path_ = Path.cwd() / "datasets" / "labelme"
best_conal = torch.load(path_ / "best_models" / "labelme_conal[scale=1e-4].pth",
map_location="cpu")
torch.save(best_conal["noise_adaptation"]["local_confusion_matrices"],
path_ / "best_models"/ "labelme_conal[scale=1e-4]_local_confusion.pth")

def highlight_max(s, props=''):
    return np.where(s == np.nanmax(s.values), props, '')

def highlight_min(s, props=''):
    return np.where(s == np.nanmin(s.values), props, '')

import json
dir_results = Path().cwd() / 'datasets' / "labelme" / "results"
meth, accuracy, ece = [], [], []
for res in dir_results.glob("modellabelme/*"):
  filename = res.stem
  _, mm = filename.split("_")
  meth.append(mm)
  with open(res, "r") as f:
    dd = json.load(f)
    accuracy.append(dd["test_accuracy"])
    ece.append(dd["test_ece"])
results = pd.DataFrame(list(zip(meth, accuracy, ece)),
                       columns=["method", "AccTest", "ECE"])
results["method"] = [
  "NS", "CoNAL[scale=0]", "CrowdLayer", "CoNAL[scale=1e-4]", "MV", "DS", "GLAD"
  ]
results = results.sort_values(by="AccTest", ascending=True)
results.reset_index(drop=True, inplace=True)
results = results.style.set_table_styles([dict(selector='th', props=[
  ('text-align', 'center')])]
  )
results.set_properties(**{'text-align': 'center'})
results = results.format(precision=3)
results.apply(highlight_max, props='background-color:#e6ffe6;',
              axis=0, subset=["AccTest"])
results.apply(highlight_min, props='background-color:#e6ffe6;',
              axis=0, subset=["ECE"])
display(results)

Table 4: Generalization performance on LabelMe dataset depending on the learning strategy from the crowdsourced labels. The network used is a VGG-16 with two dense layers for all methods.

	method	AccTest	ECE
0	MV	81.061	0.189
1	CoNAL[scale=1e-4]	85.606	0.143
2	DS	86.448	0.136
3	CoNAL[scale=0]	87.205	0.117
4	NS	87.542	0.124
5	CrowdLayer	88.468	0.115
6	GLAD	88.889	0.112

As we can see, CoNAL strategy performs best. In this case, it is expected behavior as CoNAL was created for the \texttt{LabelMe} dataset. However, using peerannot we can look into why modeling common confusion returns better results with this dataset. To do so, we can explore the datasets from two points of view: worker-wise or task-wise in Section 5.

5 Identifying tasks difficulty and worker abilities

If a dataset requires crowdsourcing to be labeled, it is because expert knowledge is long and costly to obtain. In the era of big data, where datasets are built using web scraping (or using a platform like Amazon Mechanical Turk), citizen science is popular as it is an easy way to produce many labels.

However, mistakes and confusions happen during these experiments. Sometimes involuntarily (e.g., because the task is too hard or the worker is unable to differentiate between two classes) and sometimes voluntarily (e.g., the worker is a spammer).

Underlying all the learning models and aggregation strategies, the cornerstone of crowdsourcing is evaluating the trust we put in each worker depending on the presented task. And with the gamification of crowdsourcing (Servajean et al. 2016; Tinati et al. 2017), it has become essential to find scoring metrics both for workers and tasks to keep citizens in the loop so to speak. This is the purpose of the identification module in peerannot.

Our test cases are both the \texttt{CIFAR-10H} dataset and the \texttt{LabelMe} dataset to compare the worker and task evaluation depending on the number of votes collected. Indeed, the \texttt{LabelMe} dataset has only up to three votes per task whereas \texttt{CIFAR-10H} accounts for nearly fifty votes per task.

5.1 Exploring tasks’ difficulty

To explore the tasks’ intrinsic difficulty, we propose to compare three scoring metrics:

• the entropy of the NS distribution: the entropy measures the inherent uncertainty of the distribution to the possible outcomes. It is reliable with a big enough and not adversarial crowd. More formally: \forall i\in [n_{\text{task}}],\ \mathrm{Entropy}(\hat{y}_i^{NS}) = -\sum_{k\in[K]} (y_i^{NS})_k \log\left((y_i^{NS})_k\right) \enspace.
• GLAD’s scoring: by construction, Whitehill et al. (2009) introduced a scalar coefficient to score the difficulty of a task.
• the Weighted Area Under the Margins (WAUM): introduced by Lefort et al. (2022), this weighted area under the margins indicates how difficult it is for a classifier \mathcal{C} to learn a task’s label. This procedure is done with a budget of T>0 epochs. Given the crowdsourced labels and the trust we have in each worker denoted s^{(j)}(x_i)>0, the WAUM of a given task x_i\in\mathcal{X} and a set of crowdsourced labels \{y_i^{(j)}\}_j \in [K]^{|\mathcal{A}(x_i)|} is defined as: \mathrm{WAUM}(x_i) := \frac{1}{|\mathcal{A}(x_i)|}\sum_{j\in\mathcal{A}(x_i)} s^{(j)}(x_i)\left\{\frac{1}{T}\sum_{t=1}^T \sigma(\mathcal{C}(x_i))_{y_i^{(j)}} - \sigma(\mathcal{C}(x_i))_{[2]}\right\} \enspace, where we remind that \mathcal{C}(x_i))_{[2]} is the second largest probability output by the classifier \mathcal{C} for the task x_i.

The weights s^{(j)}(x_i) are computed à la Servajean et al. (2017): \forall j\in[n_\texttt{worker}], \forall i\in[n_{\text{task}}],\ s^{(j)}(x_i) = \left\langle \sigma(\mathcal{C}(x_i)), \mathrm{diag}(\pi^{(j)})\right\rangle \enspace, where \hat{\pi}^{(j)} is the estimated confusion matrix of worker w_j (by default, the estimation provided by DS).

The WAUM is a generalization of the AUM by Pleiss et al. (2020) to the crowdsourcing setting. A high WAUM indicates a high trust in the task classification by the network given the crowd labels. A low WAUM indicates difficulty for the network to classify the task into the given classes (taking into consideration the trust we have in each worker for the task considered). Where other methods only consider the labels and not directly the tasks, the WAUM directly considers the learning trajectories to identify ambiguous tasks. One pitfall of the WAUM is that it is dependent on the architecture used.

Note that each of these statistics could prove useful in different contexts. The entropy is irrelevant in settings with few labels per task (small |\mathcal{A}(x_i)|). For instance, it is uninformative for \texttt{LabelMe} dataset. The WAUM can handle any number of labels, but the larger the better. However, as it uses a deep learning classifier, the WAUM needs the tasks (x_i)_i in addition to the proposed labels while the other strategies are feature-blind.

5.1.1 CIFAR-1OH dataset

First, let us consider a dataset with a large number of tasks, annotations and workers: the \texttt{CIFAR-10H} dataset by Peterson et al. (2019).

! peerannot identify ./datasets/cifar10H -s entropy -K 10 --labels ./datasets/cifar10H/answers.json
! peerannot aggregate ./datasets/cifar10H/ -s GLAD
! peerannot identify ./datasets/cifar10H/ -K 10 --method WAUM \
            --labels ./datasets/cifar10H/answers.json --model resnet34 \
            --n-epochs 100 --lr=0.01 --img-size=32 --maxiter-DS=50 \
            --pretrained

import plotly.graph_objects as go
from plotly.subplots import make_subplots
from PIL import Image
import itertools

classes = (
    "plane",
    "car",
    "bird",
    "cat",
    "deer",
    "dog",
    "frog",
    "horse",
    "ship",
    "truck",
)

n_classes = 10
all_images = utx.load_data("cifar10H", n_classes, classes)
utx.generate_plot(n_classes, all_images, classes)